数据结构与算法
时间复杂度、空间复杂度
时间复杂度和空间复杂度是一个非常重要的概念,对于数据结构和算法来说往往依靠这两个概念来评估它们的优劣。
大O表示法
定义:如果存在正数c和N,对于所有的n≥N,有f(n)≤cg(n),则f(n)=O(g(n))。
这个定义的问题在于:首先,改定义只证明了一定存在某个c和N,但没有说明如何求出这两个常数;其次,他没有给这些值添加任何限制,也没有说明当有多个可选值时如何进行选择。实际上,对于同一对f和g,通常可以指定无数对c和N。
——Adam Drozdek《C++数据结构与算法》(第4版)
根据这个定义引申出来的两个重要性质:
- 在多项式g(n)中,取次数最高的项为大O表示,其余项可忽略。
- 次数最高项的常数系数可以忽略。
这两个性质可以推出一些有趣的结论:
两种时间复杂度相同的代码合在一块,其时间复杂度和原来相同。(常数系数可以忽略)
时间复杂度效率比较中,对数的底的数值是可以忽略的(例如:O(log2n)=O(log3n)),所以一般取10为底。
时间复杂度的比较:O(1)<O(lgn)<O(n)<O(nlgn)<O(n2)<o(2n)<O(n!)<O(nn)
可以看到,这种定义实际上是存在问题的。大O表示法更关注算法执行的增长速率,而忽略了常数项c和N。实际上大O表示法代表了f(n)的上界。它表示在糟糕的情况下,程序需要执行的次数。所以这种效率评估方法往往更适合于大程序,而对于执行次数有限(即N并不大的情况)或者需要更精细化比较(即需要考虑常数c)的程序而言,这个评估方法就不太实用了。
大Ω表示法
定义:如果存在正数c和N,对于所有的n≥N,有f(n)≥cg(n),则f(n)=Ω(g(n))。
大Ω表示法强调了算法的下界。和大O表示法一样,都存在冗余问题(即有无数对c和N)。但是一般只有最大的下界和最小的上界才有讨论意义。
大Ω表示法和大O表示法的联系:
当且仅当g(n)=O(f(n))时,f(n)=Ω(g(n))
可以看到,无论哪种表示法都是对效率的近似表示,当确切分析某个程序的效率时,有时候需要关注细节;而对于算法本身的优劣,可以采用这些近似方法进行初步评估。对于每种数据结构,应该要掌握其创建的方法和增删查改的操作,并且要学会分析其操作的时间复杂度和空间复杂度。
数组
操作
查
只要拿到数组下标,那么查找的速度非常快。
时间复杂度:O(n)
左闭右开原则
一般来说,采用线性表结构的数据结构中,往往头指针和尾指针的指向采用左闭右开原则,即头指针指向第一个元素,尾指针指向末尾元素的下一个位置。
采取这样的策略可以简化代码量,并且某些情况下可以使得一些求值公式更直观更符合语义:
求长度时,更符合语义
length = rear - front;//若左闭右闭策略,则需要rear-front+1遍历时的方式与遍历数组时相同
for(Datatype front = begin; front < rear; ++front)//遍历的判断条件采用小于或大于号,符合习惯 { //...... }更重要的是,左闭右开原则可以减少分类讨论的可能性以及某些状态的歧义性。
例如,如果采用左闭右闭策略,序列为空和序列有一个元素时的两种情况下front和rear指针的指向是相同的。(例如栈的栈顶和栈底指针),此时需要增加代码量在进行分类讨论。
实际上链表哨兵的设计也可以理解为左闭右开原则的变种。
需要明确的是,无论左闭右开还是左闭右闭,本质上并不影响数据结构的性质,仅仅只是代码设计上的细节问题。
链表
单向链表
- 头指针Node* head*(指向首个节点的指针)*
- 节点*(包含指针域和数据域)*
构建方法
头插法
头插法插入节点的顺序与最终链表节点顺序相反
尾插法
通常来说需要多一个尾节点指针,否则构建链表的时间复杂度是O(n2)
原因:如果没有尾节点指针,那么每次插入新节点都需要遍历一次链表,插入n个节点就需要遍历n−1次
增、删、查、改
时间复杂度
O(n)
查、改操作
一般需要定义一个移动指针
pmove = head;
//...设置循环
pmove = pmove->next;
//找到自己查找或修改的节点增、删操作
增加节点必须要先明确一点:增加的节点是放在某个节点的前面还是后面。因为这会影响到循环控制变量的次数是取n还是n+1。

例如上图,有4个节点的链表中,新增链表的位置有5个,就是这个性质往往导致增加节点到1位置的情况需要分类讨论。
增加节点往往需要两个临时节点指针,pmove和tmp,pmove用来遍历链表,tmp通常是指插入的节点或者要删除的节点。(通常还喜欢用pre、cur和next来表示)
增、删的核心代码
//增
tmp->next = pmove->next;
pmove->next = tmp;//删
tmp = pmove->next;
pmove->next = pmove->next->next;//pmove->next = tmp->next;
delete tmp;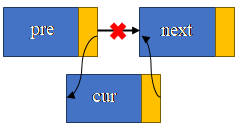
可以看到,无论增删,其中核心就是找到pre节点的地址,而不是找到next节点,因为pre->next就是next节点的地址,但是无法从next节点得知pre节点地址。
哨兵
根据上面两条核心代码可以发现,如果在第一个节点前增加新节点,那么代码将不能用,需要分类讨论
pmove = head;
tmp->next = pmove;
head = tmp;将哨兵节点放在整个链表的最前面,作用仅仅是使得代码整体优雅简洁,使得增删操作不需要分类讨论。
无哨兵版本代码
#include <iostream>
using std::cin;
using std::cout;
using std::endl;
struct Node
{
public:
Node(int d = 0, Node* n = nullptr)
:_data(d)
,_next(n)
{}
int _data;
Node* _next;
};
class Linklist
{
public:
Linklist(){}
Linklist(int n):_num(n),_head(getHead())
{
while(n-->0)
{
Node* tmp = new Node();
tmp->_data = n;
tmp->_next = _head;
_head = tmp;
}
// headInsert
}
Node* getHead(){return _head;}
~Linklist()
{
Node* tmp = nullptr;
while(_head)
{
tmp = _head->_next;
delete _head;
_head = tmp;
}
}
//节点位置采用数组下标的方式,第一个为0
void addNode(int n = 0, int data = 0)
{
if(n > _num || n < 0)
{
cout << "add position error" << endl;
return;
}
++_num;
Node* tmp = new Node(data);
Node* pmove = _head;
if(0 == n)//没有哨兵时需要对头节点分类讨论
{
tmp->_next = _head;
_head = tmp;
}
else
{
while(n-->1)//这里为什么是1
{
pmove = pmove->_next;
}
tmp->_next = pmove->_next;
pmove->_next = tmp;
}
}
void delNode(int n = 0)
{
if(n > _num - 1 || n < 0)//一件非常重要的事情:_num == 0时会发生什么?
{
cout << "delete position error" << endl;
return;
}
--_num;
Node* pmove = _head;
Node* tmp = nullptr;
if(0 == n)//没有哨兵时需要对头节点分类讨论
{
tmp = _head;
_head = _head->_next;
delete tmp;
}
else
{
while(n-->1)//这里为什么是1
{
pmove = pmove->_next;
}
tmp = pmove->_next;
pmove->_next = pmove->_next->_next;
delete tmp;
}
}
void print()
{
Node* pmove = _head;
while(pmove)
{
cout << pmove->_data << ' ';
pmove = pmove->_next;
}
cout << endl;
}
private:
int _num = 0;
Node* _head = nullptr;
};
int main()
{
Linklist a(10);
int cmd = 1;
while(cmd)
{
cout << "choose cmd: 1, 2 or 0" << endl;
cin >> cmd;
int data,pos;
switch(cmd)
{
case 1:
cout << "add: position , data" << endl;
cin >> data >> pos;
a.addNode(data,pos);
a.print();
break;
case 2:
cout << "delete: position" << endl;
cin >> pos;
a.delNode(pos);
a.print();
break;
case 0:
cout << "bye" << endl;
break;
default:
cout << "cmd error" << endl;
}
}
return 0;
}有哨兵版本代码
#include <iostream>
#include "Linklist.h"
using std::cin;
using std::cout;
using std::endl;
using Datatype = int;
struct Node
{
Node(Datatype data = 0, Node* n = nullptr)
:_data(data)
,_next(n)
{}
Datatype _data;
Node * _next;
};
class Linklist
{
public:
Linklist();
~Linklist();
bool ispos(const int& pos) const;
//将判断pos在合理范围内的命题抽象成方法,可以使代码更简介,但是同时也存在一些逻辑陷阱
void addNode(Datatype data, int pos);
void delNode(int pos);
void print() const;
private:
Node* _head;
int _size;
};
Linklist::Linklist()
:_head(new Node())
,_size(0)
{}
Linklist::~Linklist()
{
Node* pmove = _head;
Node* tmp = nullptr;
while(pmove)
{
tmp = pmove;
pmove = pmove->_next;
delete tmp;
}
}
bool Linklist::ispos(const int& pos) const
{
if(pos < 0 || pos > _size - 1)//若_size = 0,返回值永远等于false。
return false;
else
return true;
}
void Linklist::addNode(Datatype data, int pos)
{
if(ispos(pos) || pos == _size)//pos == _size条件很重要
{
Node* pmove = _head;
while(pos-->0)//这里为什么是0
{
pmove = pmove->_next;
}
Node* tmp = new Node(data);
tmp->_next = pmove->_next;
pmove->_next = tmp;
++_size;
}
else
{
cout << "addNode error" << endl;
}
}
void Linklist::delNode(int pos)
{
if(ispos(pos))//注意判断条件
{
Node* pmove = _head;
while(pos-->0)//这里为什么是0
{
pmove = pmove->_next;
}
Node* tmp = pmove->_next;
pmove->_next = pmove->_next->_next;
delete tmp;
--_size;
}
else
{
cout << "delNode error" << endl;
}
}
void Linklist::print() const
{
Node* pmove = _head->_next;
while(pmove)
{
cout << pmove->_data << " ";
pmove = pmove->_next;
}
cout << "_size:" << _size << endl;
}有哨兵版本更简洁明了,并且对插入删除的判断条件抽象成一个方法,使得代码可读性更高。
这里有几个小细节需要注意:
上面两个版本的代码,都将假设代码的编号从0开始,那么对于增操作来说,pos为0就是新增节点为头节点。
无论有无哨兵,对于长度为size的链表,删除操作中,判断pos是否合理的范围是[0,size);而增加操作中,判断pos合理范围是[0,size],所以在addNode方法中需要用if(ispos(pos)∣∣pos==size)来判断。
但是这里有一处陷阱,即size值是变化的,当size为0时显然[0,size)为空集,任何pos都不在集合内,即ispos(pos)返回值一定为false。
而巧妙的是,当size为0时,
- 对于删操作,逻辑上不可能进行删除操作,而代码中ispos(pos)一定会返回false,这是符合语义和逻辑的;
- 对于增操作,虽然ispos(pos)一定会返回false,但是pos==size的判断使得当且仅当pos==0时可以进行增操作,这同样也是符合语义和逻辑的。
代码中(pos < 0 || pos > size - 1)等价于[0, size - 1],等价于[0, size)。
双向链表
只要熟悉掌握了单向链表,双链表就不是难题。双向链表在指针域上多了指向前一个节点的指针Node* pre,所以在处理增删节点的问题上更加灵活。但是在两端节点的增删仍然需要特别处理。
例如在单向链表中在pre和next节点插入cur节点,关键是找到pre节点,这样就可以通过pre->next找到next节点了。但是在双向链表中指针域中存在pre指针,所以找到一个节点后,既可以往前插,也可以往后插,非常灵活。(可以找到next节点,并通过pre指针插入)
尽管如此,为了保持连贯性和一致性,还是建议使用单链表的思维增删改查链表。因为在代码层面上,对双向链表的操作仅仅只是在单链表的基础上修改每个节点的pre指针,非常方便。
在创建双向链表时,可以将创建过程视为单链表中头插法和尾插法同时进行。
双向链表可以增加哨兵,来简化代码。
循环链表
循环链表就是将单链表的最后一个节点的next指针从指向nullptr转换到指向第一个节点。
在创建第一个节点时,单链表的做法是将next指针指向nullptr,而对于循环链表来说只需要将这个节点的next指针指向自己。
由于循环链表无法通过pmove = nullptr这样的操作是否到达链表尾端,通常循环链表通过增加一个size变量或者一个尾指针来指定最后一个节点。
如果有哨兵,那么循环链表的最后一个节点的指针既可以选择指向哨兵,也可以直接指向第一个节点。但是要注意遍历时可能会将哨兵计算进内。
双向循环链表
没什么特别之处,就是双向链表和循环链表的结合。
双向循环链表没有必要增加哨兵。
静态链表
静态链表解决了没有指针的高级语言如何实现链表结构的问题。它的底层的物理结构是一片连续的存储空间。
为了能够实现链表的形式,通常静态链表的节点元素由数据和游标构成,即数组的一个下标对应一个数据和游标。游标的作用就是指明下一个元素的数组下标。所以由数组实现的静态链表又称为游标实现法。
至此为止,可能会觉得这和数组没有什么不同,而真正体现出静态链表和顺序表的异同在于增删操作
对于顺序表来说,中间插入或者删除元素,都需要调整后面元素的位置。而静态链表的增操作,只需要将数据放入到空闲的数组元素,并修改游标。而对于删操作,就是将对应的元素置于空闲状态。
在频繁的增删操作之后,空闲元素在数组中的位置将是非常零散的,如何快速找到零散的空闲元素?
当然我们可以通过将空闲元素的游标设置为特殊值,通过遍历查询得到空闲的元素。但这样做非常愚蠢。
解决方法:
逻辑上,在静态链表中构建两个链表结构,一个是存放数据的链表,一个未使用的备用链表。
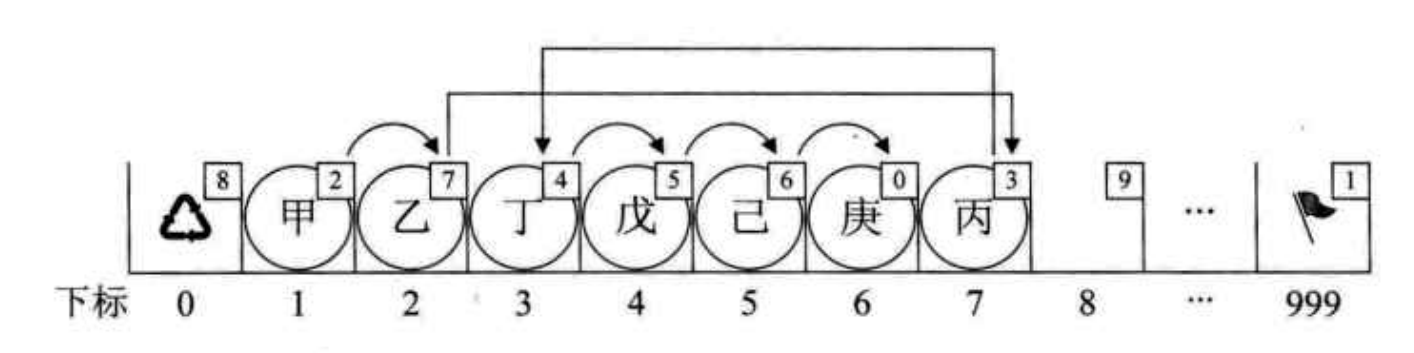
增操作:取下备用链表的首个节点,并插入到存放数据的链表中。
删操作:对删除的节点通过头插法插入到备用链表中。
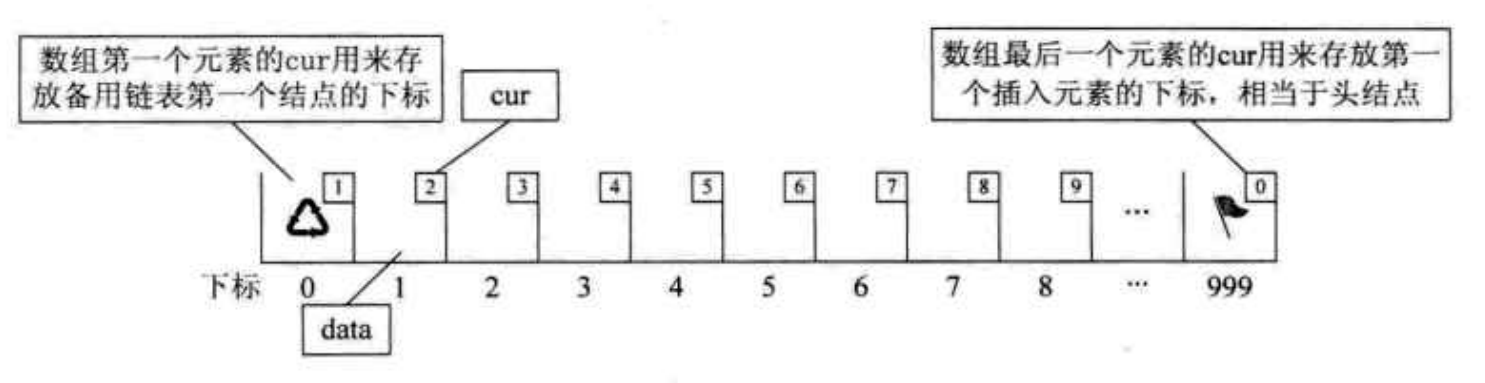
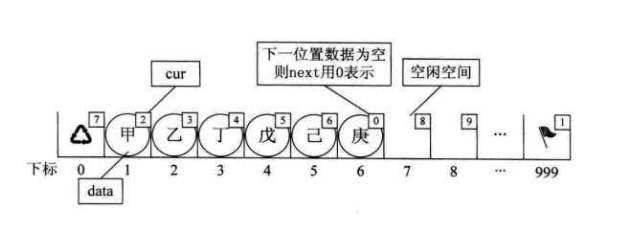
以上增删操作都涉及到游标的修改。所以一般静态链表还需要维护“两个头指针”(指向存放数据的链表和备用链表的游标),用C语言实现时通常数组的头尾两个元素不存放数据,而其游标存放这”两个头指针”。其作用类似于单链表中的哨兵。
可以看出,这个时候备用链表在操作上就像是链式存储的栈
代码实现
#include <iostream>
using std::cin;
using std::cout;
using std::endl;
using Datatype = int;
struct Node
{
Datatype _data;
int _next;
};
class Sqlist
{
public:
Sqlist(int c);
~Sqlist();
bool ispos(const int& pos) const;
bool isfull() const;
bool isempty() const;
//有限资源的存储结构需要判空、判满
void addNode(Datatype data, int pos);
void delNode(int pos);
void print() const;
void printArr() const;
private:
int _head;
int _standby;
int _size;
int _capacity;
Node* _arr;
};
Sqlist::Sqlist(int c)
:_head(0)//存放数据链表的首元素游标
,_standby(0)//备用链表的首元素游标
,_size(0)//存放数据的链表长度
,_capacity(c)//整体容量长度
,_arr(new Node[c])//底层存储结构
{
for(int i = 0; i < c; ++i)
{
_arr[i]._next = i + 1;
_arr[i]._data = -1;
}
_arr[c-1]._next = 0;//备用链表最后一个元素游标指向第一个元素下标
}
//初始化时将整个链表当作备用链表
Sqlist::~Sqlist()
{
delete [] _arr;
}
bool Sqlist::ispos(const int& pos) const
{
if(_size == 0)
{
if(pos == 0)
return true;
else
return false;
}
else
{
if(pos < 0 || pos > _size - 1)
return false;
else
return true;
}
}
bool Sqlist::isfull() const
{
if(_capacity == _size)
return true;
else
return false;
}
bool Sqlist::isempty() const
{
if(_size == 0)
return true;
else
return false;
}
void Sqlist::addNode(Datatype data, int pos)
{
if(!isfull() && (ispos(pos) || pos == _size))
{
if(pos == 0)
{
int tmp = _arr[_standby]._next;
_arr[_standby]._data = data;
_arr[_standby]._next = _head;
_head = _standby;
_standby = tmp;
}
else
{
int mov = _head;
while(pos-->1)
{
mov = _arr[mov]._next;
}
int tmp = _arr[_standby]._next;
_arr[_standby]._data = data;
_arr[_standby]._next = _arr[mov]._next;
_arr[mov]._next = _standby;
_standby = tmp;
}
++_size;
}
else
{
cout << "addNode error" << endl;
}
}
void Sqlist::delNode(int pos)
{
if(!isempty() && ispos(pos))
{
if(pos == 0)
{
int tmp = _head;
_head = _arr[_head]._next;
_arr[tmp]._data = -1;
_arr[tmp]._next = _standby;
_standby = tmp;
}
else
{
int mov = _head;
while(pos-->1)
{
mov = _arr[mov]._next;
}
int tmp = _arr[mov]._next;
_arr[mov]._next = _arr[_arr[mov]._next]._next;
_arr[tmp]._next = _standby;
_arr[tmp]._data = -1;
_standby = tmp;
}
--_size;
}
else
{
cout << "delNode error" << endl;
}
}
void Sqlist::print() const
{
int mov = _head;
for(int i = 0; i < _size; ++i)
{
cout << _arr[mov]._data << " " << _arr[mov]._next << endl;
mov = _arr[mov]._next;
}
}
void Sqlist::printArr() const
{
for(int i = 0; i < _capacity; ++i)
{
cout << _arr[i]._data << '\t';
}
cout << endl;
for(int i = 0; i < _capacity; ++i)
{
cout << _arr[i]._next << '\t';
}
cout << "_head:" << _head << " "
<< "_standby:" << _standby << endl;
cout << endl;
}栈
增、删、查、改
栈结构相比链表结构简单得多,拥有LIFO特点(last in first out)。栈结构的底层物理结构可以顺序表,也可以是链表结构。如果是链表结构,那么栈可以理解为只对首个节点进行增删操作的单链表。一个栈通常涉及到的几个方法
class Stack
{
public:
void push(Datatype data);//压栈
void pop();//弹栈
void peek() const;//查看栈顶
bool isFull() const;//判满
bool isEmpty() const;//判空
//......
private:
int _size;//元素个数
int _capacity;//栈容量
Datatype _top;//栈顶位置(或者下一个位置)
Datatype* _arr;//指向底层数据结构的指针
};- 如果底层存储结构是链表,则通常不需要isFull()方法以及_capacity数据成员。
时间复杂度
增删查改的操作都是在栈顶上进行,所以时间复杂度为O(1)。
队列
队列拥有FIFO(first in first out)特点。
常规操作
class Queue
{
public:
void enQueue(Datatype data);//入队
void deQueue();//出队
void isfull() const;//判满
void isEmpty() const;//判空
void getLength() const;//获得长度
private:
Datatype _front;//头指针
Datatype _rear;//尾指针
int _length;//队列长度
Datatype* _arr;//队列底层存储结构的指针
}需要特别强调的是:头尾指针的指向应当采用左闭右开原则策略。
顺序存储的队列
顺序存储结构的队列是指底层的存储结构是数组的队列。
队列
队列的头指针和尾指针分别在插入和删除后都会向后移动**(并且不会往前移动)**,而判断是否溢出的标准时尾指针是否到达数组末尾,这就导致了两种溢出情况:
- 上溢现象:队列已满,但仍继续入队。
- 假溢出现象:元素出列后,头指针指向下一个元素。这导致前面的存储空间浪费了,当尾指针指向队列末尾时队列内实际上还有未使用空间,故称为假溢出。
循环队列
当头指针前面还有空位时,即便尾指针到达数组末尾时,尾指针会移动到数组首位,继续填补队列直至所有位置填满。这种设计的队列称为循环队列。
注意:通常来说,循环队列的头尾指针采用左闭右开原则
但是左闭右开原则下的循环队列存在一个问题:队列为空时和队列为满时,头尾指针都指向同一个位置。
解决方案:
- 设置一个flag,分别标识队空队满的状态
- 尾指针指向的地方不存数据,即队满时数组中有个空着的位置。
现在根据解决方案2给出队列的代码
void CircularQueue::isfull() const
{
if((_rear + 1)%sizeof(_arr) == _front)//该公式囊括了队满的两种情况
return true;
else
return false;
}
void CircularQueue::isempty() const
{
if(_rear == _front)
return true;
else
return false;
}
void CircularQueue::enQueue(Datatype data)
{
if(!isfull())
{
_arr[_rear] = data;
_rear = (_rear + 1)%sizeof(_arr);//通过取余运算解决循环问题
}
}
void CircularQueue::deQueue() const
{
if(!isempty())
{
_front = (_front + 1)%sizeof(_arr);//通过取余运算解决循环问题
}
}
void CircularQueue::getLength() const
{
return (_rear - _front + sizeof(_arr))%sizeof(_arr);//根据取余运算性质避免分类讨论
}这里主要考察取余运算的灵活应用。
链式存储的队列
底层存储结构可以采用单链表的形式,并增加有个尾指针,通过封装头插法和尾插法就可以实现队列。
双端队列
使用双向链表即可实现。
树
树结构的数据结构本身不是线性的,而且形态多样,所以增删操作并不像链表、栈、队列一样方便简单。树结构往往是用来描述数据间的逻辑关系,相比增删操作,查改操作相对更重要一些。
树的定义
树是一个由n(n≥0)个节点构成的有限集合。当n=0时,为空树;当n>0时,为非空树。
任意一颗非空树都满足:
- 有且仅有一个根节点。
- 除了根节点外的其余节点可分为m(m>0)个互不相交的有限集合,每个集合本身又是一颗树。这些集合又称为根的子树。
可以看到,树是通过递归定义的。
相关概念名词
- 根
- 子树
- 叶子
- 内部节点:除根和叶子外的节点
- 分支节点:度大于0的节点
- 终端节点:就是叶子节点另一个称呼
- 树的度
- 节点的度
- 树的深度(高度)
- 节点的层次:(根的位置为树的第一层)
- 路径
- 路径长度
- 双亲
- 孩子:节点的子树的根。(要区分孩子和子孙的概念)
- 兄弟
- 堂兄弟:双亲是兄弟的节点互称为堂兄弟。(堂兄弟之间的路径长度为4)
- 祖先:从节点到整颗树的根所经过所有节点称之为该节点的祖先。
- 子孙:节点的子树中的所有节点。
- 有序树、无序树:节点的孩子的排列有次序的树,称为有序树。
- 森林:不相交的树组成的集合
- 二叉树:每个节点最多有两个孩子的树。
- 完全二叉树:除了最后一层,每一层的节点都是满的。
- 满二叉树:每一层的节点都是满的。
- 斜树、左斜树、右斜树:只有左子树或者只有右子树的树
- 二叉链表
- 二叉搜索树、二叉查找树、二叉排序树
- 二叉平衡树(AVL树)
- 最小二叉平衡树
树的存储
顺序存储
利用顺序存储的树,往往不考虑增删操作,其目的是为了用来存储节点之间的逻辑关系。
利用顺序存储的树,和静态链表的方法类似,每个节点都有数据域和指针域。
具体有以下方法:
双亲表示法
指针域保存的是双亲的下标
孩子表示法
指针域保存的是孩子的下标,但是由于每个节点的度未知,所以一般假设树的度就是每个节点的度。这就导致了空间资源浪费的问题。
双亲孩子表示法
在孩子表示法基础上每个节点增加指向双亲的位置,同样有空间资源浪费的问题。
链式存储
使用链式存储,如果采用异构型的数据结构,每个节点指针域个数按照个数分配,则描述起来非常困难;如果按照树的度来确定指针域的个数,则浪费空间。通常采用两种方式
孩子链表表示法
设置一个数组,每个元素维护一个数据域和指针域,树的所有节点的数据都放在数据域中。指针域采用链表的方式,挂载着该节点的孩子的下标。
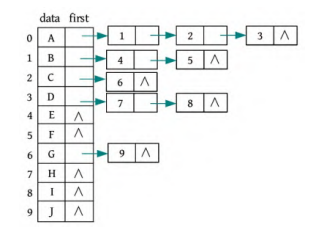
在链表的表头中加上一个双亲域,则称为双亲孩子链表表示法。
孩子兄弟表示法
每个节点有两个指针域:一个指针域保存自己的第一个孩子,另一个指针保存自己的右兄弟。那么整棵树都能通过这个方法唯一表示出来。(假设这是有序树)
这个方法有个非常优良的性质:指针域只有两个。这个方法又称为二叉树表示法。某种意义上所有的树或者森林都可以用二叉树来表示。这意味二叉树的研究有着非常重要的意义。
二叉树
通常认为二叉树的指针域中只有两个,一个指向左孩子,一个指向右孩子。
为什么不设置指向双亲的指针域呢?因为有足够的算法,即便没有指向双亲的指针,同样可以进行遍历查找等等行为。
从根节点来看二叉树,可以分为五种形态:
- 空树
- 只有根
- 只有左子树
- 只有右子树
- 有左右子树
二叉树的性质
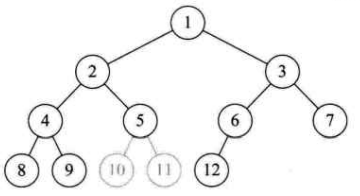
在谈二叉树性质之前,给出一点规定:如果要将树的节点进行编号,那么我们假设根的标号为1,并以层次遍历的顺序从上到下、从左到右依次编号。
性质:
第k层最多有2k−1个节点。(k≥1)
深度为k的满二叉树有2k−1个节点。(k≥1)
二叉树度为0的节点数n0和度为2的节点数n2的关系:n0=n2+1
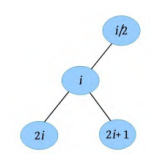
对于完全二叉树中的一个编号为i的节点,如果其有孩子,那么左孩子编号为2i,右孩子编号为2i−1。
完全二叉树中,叶子数n0和节点总数S的关系:若S为奇数,则n0=2S+1。若S为偶数,则n0=2S。
已知完全二叉树的总节点数为n,则树的深度为⌊log2n⌋+1。
关于第三条性质的证明:
如上图,假设度为0、1、2的节点数为n0、n1、n2。总节点数为S,分支数(即两个节点之间的连线)为K,则有
n0+n1+n2=S(1)
下面关于分支数的研究
自顶向下看,度为2的节点拥有两个分支,度为1的节点拥有一个分支,度为0的节点没有分支,则
n1+2n2=K(2)
从下往上看,除了根节点外,每个节点都有一个分支连接着双亲,所以
S−1=K(3)
(1)(2)(3)结合,得到
n2+1=n0(4)
第五条是第三条的推论:
完全二叉树中,度为1的节点数只能是1或者0,所以可以分类讨论,将n1=1或0带入上述公式中即可得到结论。
二叉树的遍历
二叉树的遍历是一个非常重要的内容,由于树的定义本身就是一种递归,所以通常来说二叉树的遍历涉及大量的递归算法或者迭代算法。
深度优先遍历(DFS算法):depth first search
- 前序遍历
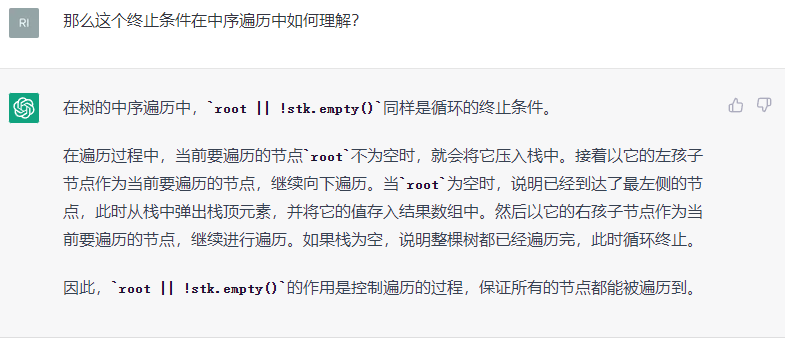
- 中序遍历
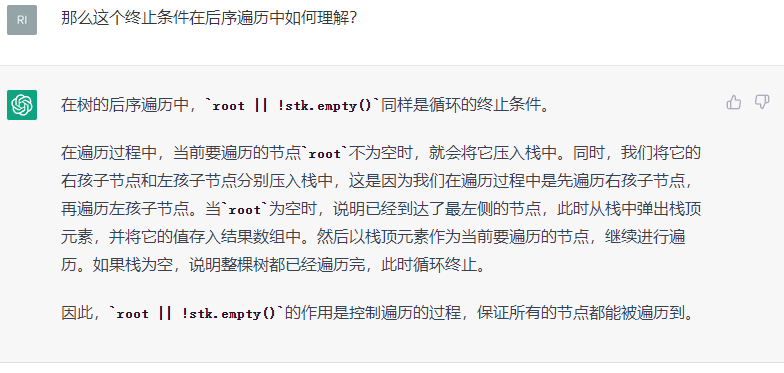
- 后续遍历
广度优先遍历(BFS算法):breadth first search
- 层次遍历
递归算法遍历
vector<int> Traversal(TreeNode* root vector<int>& ret)
{
if(!root)
{
return ret;//输出遍历序列
}
//core area
ret.push_back(root->val);//1
preorderTraversal(root->left);//2
preorderTraversal(root->right);//3
//core area
return ret;
}非常简洁简单,而中序遍历和后序遍历只需要将1、2、3的位置进行调整即可。
迭代法遍历
迭代法遍历实际上是有许多种方式。共同点都是要利用栈结构。
例如在前序遍历中,可以按照根压入、弹出,右孩子压入,左孩子压入,弹出,右孩子弹出的思想,也可以模仿递归中函数栈,先不断将左孩子压入的思想来编写代码。
以下这种遍历方法使得前、中、后序遍历代码统一,但牺牲了空间复杂度。
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<pair<TreeNode*, int> > stk;
stk.push((make_pair(root, 0)));
while(!stk.empty()) {
auto [node, type] = stk.top();//结构化绑定
stk.pop();
if(node == nullptr) continue;
if(type == 0) {
stk.push(make_pair(node->right, 0));
stk.push(make_pair(node, 1));
stk.push(make_pair(node->left, 0));
}
else result.emplace_back(node->val);
}
return result;
}
};chatGPT给出的简洁代码
//前序遍历
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while (root || !stk.empty()) {
while (root) {
res.push_back(root->val);
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
root = root->right;
}
return res;
}
//中序遍历
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while (root || !stk.empty()) {
while (root) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
res.push_back(root->val);
root = root->right;
}
return res;
}
//后序遍历
vector<int> postorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
TreeNode* lastVisited = nullptr;
while (root || !stk.empty()) {
while (root) {
stk.push(root);
root = root->left;
}
root = stk.top();
if (root->right && root->right != lastVisited) {
root = root->right;
} else {
res.push_back(root->val);
lastVisited = root;
stk.pop();
root = nullptr;
}
}
return res;
}
层次遍历
先将根节点压入队列中,每当队列元素出队时,将其孩子压入队列中,当队列为空时,遍历结束。
vector<int> levelOrderTraversal(TreeNode* root)
{
queue<TreeNode*> que;
vector<int> res;
if(!root) return res;
que.push(root);
while(!que.empty())
{
root = que.front();
res.emplace_back(root->val);
que.pop();
if(root->left) que.push(root->left);
if(root->right) que.push(root->right);
}
return res;
}二叉排序树
其特点:
- 左子树所有节点的值一定比当前子树根节点的值小,右子树所有节点的值当前根节点的值大。
- 根据上述定义,不能有相同值的节点
- 插入的新节点永远是叶节点。
- 通过二叉排序树查找时,和遍历不相同的点在于,查找会一直往下一层深入,而不会回头。
基于第四点,我们可以看出而二叉排序树的查找效率取决于树的深度。二叉排序树因其排序的原因,查找一个节点时就不必遍历整颗树。可以根据当前节点的值与要查找的值进行大小比较来查找值。所以二叉排序也称二叉搜索树,二叉查找树,他是平衡树概念的基础。
他的查找性能比普通的二叉树要高。但是,想象一下,对于一组有序序列,实际上可以对应有非常多种不同形态的二叉排序树。例如
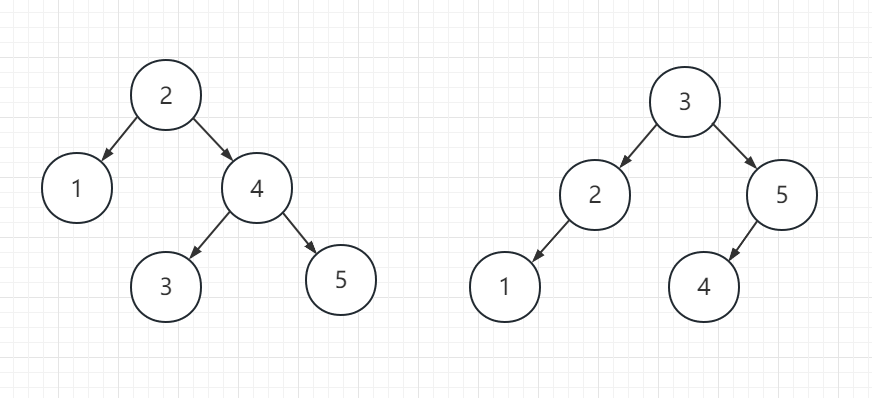
对于序列12345,上述两种二叉排序树的形态就不一样。不一样的形态往往会导致不一样的查找性能。例如
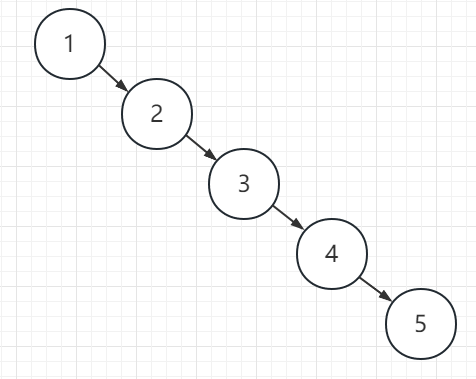
斜树也算是一种二叉排序树,但是其实与链表没有什么不同,查找的时间复杂度为O(n)。明显要比上面两种二叉树查找性能要差,这就引出了二叉平衡树。
二叉平衡树(AVL树)
先介绍一个概念:
平衡因子:一个节点的平衡因子 = 该节点的左子树深度减去右子树深度
二叉平衡树是一种二叉排序树,其特点是
- 任何节点的平衡因子的绝对值不大于1
- 插入新节点可能需要对树的位置重新调整
根据特性1,二叉平衡树的每一个节点左右子树的节点总数差不会很大,那么查找时每深入到下一层,排除掉的节点数就会趋近于一半,这和二分查找的数学原理是很相像的,而特性2保证了对二叉平衡树的插入删除节点时对特性1不变,所以AVL树的查找性能非常好。接近于二分查找的性能。
B树
B树也是一种平衡树,其节点的度大于2。B树的节点的度是一个范围值,节点能取到最大值m,则称之为m阶B树。
每个节点内可以存储多个数据,其中一个数据中应当有一部分用于给树的节点排序作判断,这个用于做判断的数据称之为key值。也就是说,B树中数据所在位置直接就是在节点当中。
从逻辑上讲(注意不是从实现层面),两个数据之间存储这一个指针,指向一个子节点,并且这个子节点的key值范围在这两个数据key值内。并且左边界数据和右边界数据应当也有指针指向子节点。(相当于数据用指针间隔)
将一个数据称之为一个元素,现在m阶B树有以下特点:
- 所有叶子节点都在同一层
- 每一个内部节点最少有
(m/2)-1个元素(向上取整),最多有m-1个元素。 - 内部节点中:子节点个数 = 元素个数 + 1
- 如果根节点不是叶子节点,那么其至少有连个子节点
B+树
红黑树
查找算法
二分法
问题:在一个无重复元素有序数组中查找某个元素的位置,若不存在则返回-1。
核心思想
- 该数组是经过排序的。
- 每次将查找值和数组中位元素进行比较,如果是则返回,如果不是则二分缩减搜索范围。
//左闭右闭区间写法
int binarySearch1(const int* arr, const int size, const int val)//假设该数组升序排列
{
int lo = 0, hi = size - 1, mid;
while(lo <= hi)//左闭右闭区间,
{
mid = lo + (hi - lo)/2;//这种写法可以防止两大数相加导致溢出
//或者:mid = lo + (hi - lo) >> 1
if(arr[mid] < val)
{
lo = mid + 1;
}
else if(arr[mid] > val)
{
hi = mid - 1;
}
else
{
return mid;
}
}
return -1;
}
//左闭右开区间写法
int binarySearch2(const int* arr, const int size, int val){
int lo = 0, hi = size, mid;//左闭右开区间,所以初始ni == size
while(lo < hi){//左闭右开区间,lo == hi是没有意义的。
mid = lo + (hi - lo)/2;
if(arr[mid] < val){
lo = mid + 1;
}
else if(arr[mid] > val){
hi = mid;//左闭右开区间,mid本身就不会被搜索
}
else return mid;
}
return -1;
}两个需要注意的方面:
mid的具体位置。
对于长度为偶数的数组,mid是对半开后靠前置的位置。例如长度为6的数组,那么mid的位置是3。注意,由于数组下标从0开始,那么就是(0+5)/2=2(整型除法),下标为2即第三个位置。而对于长度为奇数的数组,mid位置就是恰好为中间位置。
mid加1还是减1?如何决定继续在左边还是右边的范围内查找?
这其实涉及到数据的排序是升序还是降序。对于升序数组,若arr[mid] < val,则说明[0, mid]范围内的数都比val小(因为这个范围内arr[mid]为最大值),所以这个范围都被舍弃。所以排序方法以及arr[mid]和val大小判断条件决定了下一次判断的边界条件。
以下分析基于左闭右闭写法来讨论
这个讨论是为了找到val在哪两个区间之间
当arr中不存在val,二分法搜索到最后会出现以下现象:
跳出循环后lo和hi这两个下标是相邻的,并且hi比lo要小1。
通过一些特殊长度的arr来分析二分法执行到最后可能出现的状况
如果arr长度为1:
//此时lo和hi会重叠。lo = hi = mid如果arr长度为2:
//此时lo和mid是重叠的,hi比lo大1。 //if(val > arr[mid]) //{ //lo = mid = hi;再执行一次循环体 //} //if(val < arr[mid]) //{ //hi = mid - 1; //由于此时mid == lo,即hi = lo - 1; //}
当前查找范围长度为奇数时,下一次搜索范围必然是偶数,以mid为界左右两边的长度均为偶数。
当前查找范围长度为偶数时,下一次查找范围取决于val与arr[mid]的判断,mid左边为奇数,右边为偶数。
时间复杂度
最坏情况:O(lgn)
这个很好推出,假设数组长度为n,每次查找将舍弃一半的数组,最坏情况是最后才找到该元素,即(2n)x=1,求得f(x)=O(lgn)
局限性:
- 二分查找对应的数据结构必须是顺序表,即数组。
- 数据量小时没必要使用二分查找,数据量大时不适用。(受限于其存储的数据结构)
- 数据必须进行排序。
排序算法
排序算法有很多,学习排序算法关键是理解其思想,并懂得其时间复杂度以及具体代码如何实现。
以下排序默认升序,所以解释以升序为标准。
为了能简单明了的解释排序的手法,我们将元素交换写成函数:
void swap(int* a, int* b){
int tmp = *a;
*a = *b;
*b = tmp;
}冒泡排序
从头开始,相邻元素两两比较,顺序错误则进行交换,一次遍历以后最大者将沉底,并且该位置不再进行改动。
重复以上操作直至没有位置可改动。
特点:第一次外层循环结束时,最大值将沉底,次序从后往前逐渐捋顺。
void test(int* arr, int size){
while(size-->1){
for(int i = 0, j = 1; j <= size; ++i, ++j){
if(arr[i] > arr[j]){
swap(&arr[i], &arr[j]);
}
}
}
}选择排序
思路也简单,从左往后开始扫描,选出最小值放在第一个位置后,从下个位置开始再次从左往后扫描,找到最小值放在第二个位置……以此类推。
特点:最外层循环,
void test(int* arr, int size){
for(int i = 0; i < size; ++i){
for(int j = i + 1; j < size; ++j){
if(arr[i] > arr[j]){
swap(&arr[i], &arr[j]);
}
}
}
}插入排序
思路很简单,就像是打麻将,从左往后扫,遇到顺序不对的牌向前交换至正确位置。
特点:有点类似冒泡和选择排序的结合,次序从前往后逐渐捋顺。
void test(int* arr, int size){
for(int i = 1; i < size; ++i){
int k = i;//
for(int j = i - 1; j >= 0; --j){
if(arr[j] > arr[i]){
swap(&arr[i], &arr[j]);
--i;
continue;
}
else{
i = k;
break;
}
}
}
}
//注意到一个问题,当发生交换时,i会发生变化
//因为i往前的序列顺序是正确的,所以即便没有k的引入,一样正确。
//但是这样会导致一个问题,i会重复比较,这是不好的,所以可以引入k值进行优化希尔排序
快速排序
分治思想。选取基准值(一般选取数组第一个元素),准备两个指针放排序数组的两端,相向扫描。
右指针从右往左扫描,遇到比基准值小的值时停下。
左指针从左往右扫描,遇到比基准值大的值时停下。
交换两者。
重复以上三步操作,直到两个指针相遇。
此时左指针扫描过的值都比基准值要小(或等于),而右指针扫描过的值都比基准值要大(或相等),这意味着基准值的位置就是这两段区域之间,即找到了基准值的位置。
递归以上所有操作。
void test(int* arr, int size){
quickSort(arr, 0, size-1);
}
void quickSort(int* arr, int lo, int hi){
if(lo > hi) return;
int i = lo;
int j = hi;
int pivot = arr[lo];
while(i < j){
while(arr[j] >= pivot && i < j) --j;//这两个内层循环不可以交换顺序
while(arr[i] <= pivot && i < j) ++i;
if(i < j) swap(&arr[i], &arr[j]);
}
swap(&arr[lo], &arr[i]);//基准值所在位置决定了执行两个内层循环的先后顺序
quickSort(arr, lo, i-1);
quickSort(arr, i+1, hi);
}重点:内层循环不可交换顺序,必须要移动右指针,才能移动左指针。
思考两个问题:
- 左指针和右指针什么情况下会停止移动?(跳出对应的内层循环?)
左指针:遇到比基准值大的。右指针:遇到比基准值小的。
- 跳出外层循环时
i和j的相对位置是怎样的?
只有i和j相等时才能跳出循环。
- 交换前基准值在什么区域?
交换前基准值所在位置应当是小于等于基准值的区域。这意味着与它进行交换的值必须小于等于它,即当i = j时,他们指向的值必须小于等于基准值。
左右指针相遇有两种情形:
左指针移动遇到右指针。当左指针在运动,这意味着右指针停下来了,参考上方第一个问题,此时右指针指向比基准值要小的值,符合条件。
右指针移动遇到左指针。当右指针在运动,根据循环的执行顺序可以看到,虽然先前左指针停在了比基准值要大的位置,但是下一步立即进行了交换。所以此时左指针指向一个比基准值要小的位置,符合条件。
当然有一种特殊的可能,即第一次进入循环后,右指针直接运动与左指针相遇,没有发生交换,但是此时左指针指向的就是基准值,所以不会发生错误
如果while(arr[j] >= pivot && i < j) --j;和while(arr[i] <= pivot && i < j) ++i;交换顺序,那么上面第一种情形就会出错。左指针停在了一个比基准值要大的地方,右指针与其相遇后,将该值放在了比基准值要小的区域,这就发生了错误。
归并排序
堆排序
计数排序
动态规划算法
动态规划通常和递推公式相关,核心思想是将大问题拆分为为小问题。例如经典的斐波那契数列的求解:
f(x)=f(x−1)+f(x−2)
此时只要设定边界条件f(0)=0和f(1)=f(2)=1,那么问题就可以得到解决。
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?这个问题就是经典的动态规划问题。假设第n阶的答案以f(n)表示,想象一下,到第n个台阶的最后一步只有两种方式:从第n-1阶到达,或者从第n-2阶到达。所以问题就可以转化为f(n)=f(n-1)+f(n-2)
两个字符串“00”和“111”拼接为长度为n的字符串,请问有多少种字符串?
